Uma pandemia aflige o mundo fictício da nossa história e um certo medicamento foi inicialmente sugerido como potencial tratamento para a doença. Estudos clínicos randomizados serão conduzidos nesse mundo fictício para testar se o medicamento funciona.
O medicamento tem 30% de eficácia para reduzir a incidência de um certo desfecho ruim. Eu sei disso porque eu sou o criador desse mundo e eu que decido, quer dizer, eu que escrevi o código das simulações que vão gerar os resultados dos estudos clínicos randomizados conduzidos nesse mundo e a eficácia é o que eu decidi que seria, o que eu coloquei no código. Eu decidi também que todos os estudos randomizados seriam conduzidos sorteando pacientes de uma população em que o desfecho ruim tem probabilidade de 10%; desse modo, no grupo controle dos estudos, a probabilidade de um desfecho ruim será de 10% e no grupo tratado a probabilidade de um desfecho ruim será de 7%. Note que 7/10 = 0.7 é o chamado risco relativo, que corresponde a uma eficácia de 1 – 0.7 = 0.3 ou 30%, como eu havia dito.
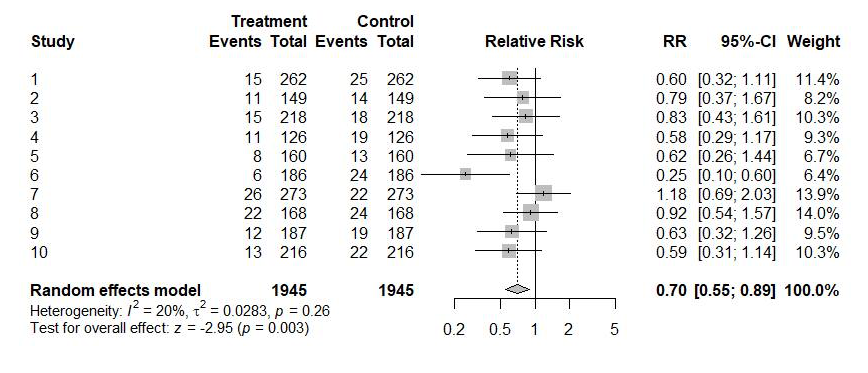
Ao longo de toda a nossa história fictícia, foram conduzidos dez estudos randomizados e os resultados obtidos estão ilustrados na primeira imagem.
Trata-se de um forest plot que apareceu numa metanálise publicada ao final da história. Cada linha do forest plot corresponde a um estudo. Do lado esquerdo aparecem o número de pacientes e o número de pacientes que tiveram um desfecho ruim no grupo tratado e no grupo controle. Do lado direito, aparece o risco relativo estimado por aquele estudo, juntamente com um intervalo de confiança de 95%, mais popularmente conhecido como margem de erro. Na coluna mais à direita aparece o peso com que o estudo entrou na metanálise que foi publicada ao final da história.
Recorde que a eficácia é igual a 1 menos o risco relativo. Um risco relativo igual a 1 corresponde a nenhuma eficácia (o tratamento não faz diferença alguma) e um risco relativo menor do que 1 corresponde a um tratamento que beneficia os pacientes – quanto menor o risco relativo, maior a eficácia. Já um risco relativo maior do que 1 corresponde a um tratamento que prejudica os pacientes – quanto maior, mais prejudica.
Os habitantes desse mundo não sabem a eficácia real da droga e tentam se basear nos dados desses estudos para estimá-la. O risco relativo real é 0.7 (correspondente a uma eficácia de 30%) – eu, criador da simulação, sei disso. Os valores de risco relativo que os habitantes desse mundo observam nos estudos são estimativas desse valor real, flutuam em torno dele. Em nove dos dez estudos, o grupo tratado se saiu melhor do que o grupo controle, mas em um deles (estudo número 7) o grupo controle se saiu melhor; nesse estudo, a incidência de desfechos ruins foi 18% maior no grupo tratado. Apesar disso, é um fato que o medicamento reduz em 30% o risco de um desfecho ruim.
Em apenas um estudo o resultado obtido foi estatisticamente significativo, isto é, o p-valor ficou abaixo de 0.05; trata-se do estudo número 6, em que a eficácia foi muito superestimada (75% em vez de 30%, que é o valor real) e o intervalo de confiança não corta a linha vertical correspondente a ausência de efeito (risco relativo igual a 1). Eu, criador desse mundo e conhecedor do risco relativo real de 0.7, sei que nesse estudo não foi nem o caso que o intervalo de confiança de 95% contém o valor real do risco relativo (sim, isso é possível e acontece em média 5% do tempo).
Os p-valores obtidos nos dez estudos foram os seguintes (teste exato de Fisher bicaudal): (1) 0.138; (2) 0.677; (3) 0.718; (4) 0.173; (5) 0.367; (6) 0.001; (7) 0.651; (0.874; (9) 0.260; (10) 0.158.
Com exceção do estudo número 6, os p-valores são consideravelmente maiores do que 0.05, vários realmente bem maiores.
Esse mundo é parecido com o nosso em um aspecto: os cursos de estatística para estudantes de ciências biológicas são ruins e os autores dos estudos têm o hábito de escrever nas conclusões dos seus artigos que “não houve diferença entre o grupo tratado e o grupo controle” ou que “o medicamento não reduziu a incidência do desfecho ruim” nos estudos em que o p-valor foi maior do que 0.05. Associações de estatísticos já alertaram que as conclusões não deveriam ser escritas dessa maneira, mas ninguém dá muita atenção a eles. Alguns autores até já aprenderam a interpretar os resultados corretamente, mas a maioria não, continuam pensando e escrevendo do jeito errado que estão acostumados. “Assim aprendi”, explica um deles.
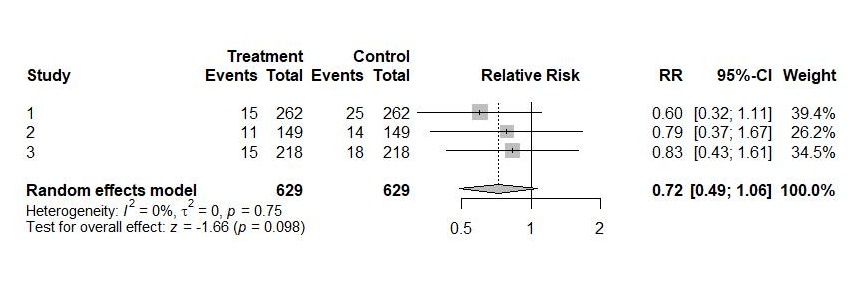
Como uma pandemia está em curso, muitos ditos “especialistas” dão entrevistas frequentemente para a imprensa. Sempre os mesmos, em geral. Eles repetem feito papagaios as conclusões dos autores (“se o próprio autor disse isso, quem sou eu para contestar”) e também compartilham de suas confusões. Depois que foi publicado o primeiro estudo, com p-valor=0.138, explicaram eles: “resultado negativo, o medicamento não ajudou os pacientes tratados”. Depois que foi publicado o segundo, com p-valor=0.677, eles estavam ainda mais convencidos: “claramente não funciona, vamos parar de perder tempo estudando isso”. Depois que foi feito o terceiro estudo, algum grupo decidiu publicar uma metanálise (veja o segundo forest plot ilustrando o post); p-valor = 0.098, não funcionou. “Esse é o prego no caixão desse medicamento”, comentou alguém.
E assim se sucedeu. Depois de dez estudos realizados ao longo de muito tempo, nove ciclos de notícias com manchetes: “estudo mostra que o medicamento não funciona”, com “especialistas” dando entrevistas explicando isso. Teve aquele estudo número 6 em que a conclusão diz que funciona, mas é um ponto fora da curva, ninguém deu muita bola. “Trata-se de um estudo metodologicamente falho”, explicou um “especialista”. Para piorar, houve também outros estudos além dos dez – que não aparecem na ilustração – em que o medicamento foi usado de forma inadequada, na fase errada da doença, com a dose errada. Esses outros estudos também geraram ciclos de notícias com “especialistas” afirmando que o medicamento não funciona: “Afinal, ou funciona ou não funciona, isso de usar de forma inadequada é uma desculpa dos negacionistas que ainda insistem em defender o medicamento. Além do mais, mesmo nos estudos em que o medicamento foi usado da forma que eles acham que tem que usar, não foi encontrada qualquer evidência de eficácia”, explica o Presidente do Instituto Eu Sou a Ciência, que está sempre dando entrevistas.
Toda vez que a imprensa falava do medicamento, falava que era um “medicamento comprovadamente ineficaz”. O assunto já havia virado piada. Obviamente só terraplanistas poderiam continuar defendendo um medicamento cuja ineficácia foi comprovada por tantos estudos.
Um dia, depois do décimo estudo, foi publicada uma nova metanálise, com o forest plot maior que ilustra o post. P-valor igual a 0.003. Estimativa pontual de risco relativo de 0.7 (eu, criador desse mundo fictício, sei que acertaram em cheio), com intervalo de confiança de 95% indo de 0.55 a 0.89. Os autores dessa metanálise têm de fato uma formação boa e escreveram no artigo uma tremenda bronca na comunidade científica e na mídia que passou dois anos tratando resultados sem significância estatística como evidência de ineficácia, algo que atrapalhou até o recrutamento de pacientes para novos estudos.
Agências checadoras de fatos convocaram então os seus “especialistas” para comentar o assunto. Continuaram repetindo que, como o gráfico na própria metanálise mostra, há 9 estudos que afastaram a eficácia do medicamento: “veja como o intervalo de confiança corta a linha vertical, indicando ausência de eficácia”, explicaram. “O único estudo que encontrou efeito é aquele estudo número 6, metodologicamente falho. A metanálise é só uma salada que mistura vários estudos tentando expremer alguma eficácia de algo que não tem nenhuma”, explicam. Conclusão: FALSO, a metanálise não prova nada. Podemos todos dormir com a consciência tranquila, afinal ninguém morreu à toa.