Recentemente foi noticiada pelo Médicos Pela Vida a publicação de uma metanálise de estudos randomizados afirmando que a vitamina D reduz a internação em UTI de pacientes de covid. Essa metanálise possui a característica curiosa de dizer em seu título que a evidência é “definitiva”. O termo foi replicado pela notícia do Médicos Pela Vida. Não pretendo aqui fazer uma revisão da metanálise nem discutir possíveis limitações dos estudos incluídos. Meu propósito é apenas o de explicar em que sentido a metanálise seria “definitiva”. Isso está ligado a uma técnica utilizada pelos autores chamada Trial Sequential Analysis.
Antes de mais nada, deve-se esclarecer que não existe em Ciência nada que seja literalmente comprovado ou definitivo. Nem as melhores teorias da Física são definitivas, embora produzam predições experimentais de acurácia extraordinária numa variedade enorme de contextos. Não seria então a Ciência Médica, que por sua própria natureza tem muito mais incertezas que a Física, que iria produzir uma evidência definitiva de algo.
No entanto, quem compreende as técnicas utilizadas pelos autores da metanálise sobre vitamina D entende porque eles se expressaram desse jeito. A seguir, fazemos uma breve exposição dos temas relevantes.
O problema das comparações múltiplas
Em estatística, quando fazemos um teste de hipóteses, nós colocamos critérios para rejeição da chamada hipótese nula que limitam a nossa probabilidade de cometer o erro de rejeitá-la por engano. Um valor comumente usado para esse limitante é 5%, isto é, o famoso p-valor < 0.05. Assim, por exemplo, quando realizamos um estudo clínico, nós adotamos um critério para afirmar que a droga é eficaz de forma que teremos uma probabilidade não superior a 5% de afirmar erroneamente que ela é eficaz.
O que acontece se num mesmo artigo científico nós testamos várias hipóteses e para todas elas adotamos esse critério de rejeição que limita em 5% a probabilidade de uma rejeição errônea? Enquanto é verdade que para cada hipótese testada haverá esse limite de 5% para a probabilidade de uma rejeição errônea, a probabilidade de que o artigo rejeite erroneamente pelo menos uma das hipóteses estudadas será em geral bem mais do que 5%.
Esse é o chamado problema das comparações múltiplas. O problema não se limita ao conteúdo de um único artigo científico. Se temos uma pilha enorme de artigos científicos e cada um deles tem apenas uma probabilidade de 5% de rejeitar erroneamente sua hipótese nula, a probabilidade de que ao menos um dos artigos científicos tenha uma conclusão errada é alta.
Estudos clínicos com análises interinas
Quando se escreve um protocolo para a realização de um estudo clínico muitas vezes são planejadas análises interinas dos dados. Numa análise interina poderia se descobrir, por exemplo, que há muitos efeitos adversos graves no grupo tratado e que o estudo deve ser interrompido por questões de segurança. Ou então poderia se descobrir que o grupo tratado está tendo resultados muito similares aos do grupo controle ou que o número de eventos observados no estudo é muito pequeno, de modo que seja muito improvável que se obtenha um resultado positivo e estatisticamente significativo ao final do estudo com o tamanho de amostra originalmente planejado. Nesse caso o estudo seria interrompido por futilidade. Finalmente, pode-se descobrir que o tratamento está funcionando tão bem que o estudo é interrompido e você passa a tratar também o grupo controle.
Ocorre que análises interinas produzem um problema de comparações múltiplas. De fato, cada análise interina leva a um teste de hipótese. Se for decidido interromper o estudo e declarar vitória desde que em ao menos uma análise interina seja obtido um resultado estatisticamente significativo (p < 0.05), a probabilidade de concluir por engano que a droga funciona será maior do que 5%.
Existem métodos padrão para lidar com o problema das comparações múltiplas em análises interinas, o mais popular utiliza algo chamado alpha spending function. O assunto é um tanto técnico para ser tratado aqui em detalhes, mas a ideia é que o critério de parada em cada análise interina deve ser bem mais rigoroso do que apenas p < 0.05, de modo a garantir que a probabilidade de se concluir erroneamente que a droga funciona após todas essas análises nunca ultrapasse 5%.
Metanálises e comparações múltiplas
Quando realizamos uma metanálise, combinamos diversos estudos clínicos sobre uma intervenção para obter uma estimativa da sua eficácia que é mais precisa do que as estimativas produzidas por cada estudo individualmente. Em particular, pode ser que cada estudo incluído seja pequeno e não tenha um resultado estatisticamente significativo, mas que quando combinamos todos os estudos obtenhamos um p-valor menor do que 0.05.
Ocorre que frequentemente fazemos muitas metanálises sobre um mesmo tema. Por exemplo, talvez alguém tenha feito uma primeira metanálise quando havia apenas 3 estudos sobre a intervenção, depois fizeram outra quando tinha 7 estudos, depois fizeram outra quando tinha 13 estudos, e assim por diante. Esse tipo de coisa é comum: as metanálises que estão na Cochrane Library são atualizadas de tempos em tempos, levando em conta novos estudos que foram realizados desde a última atualização.
Note que caímos aí num problema de comparações múltiplas similar àquele que ocorre quando se faz análises interinas de um único estudo clínico. Cada metanálise nova que é feita quando novos estudos são incluídos pode ser vista como uma análise interina de um grande estudo hipotético que engloba todos os estudos que serão feitos sobre aquele tema ao longo da história. Existe então uma preocupação de que essas múltiplas comparações levem a uma probabilidade de concluir erradamente que a droga funciona que seja maior do que 5%.
A técnica conhecida como Trial Sequential Analysis foi desenvolvida para lidar com esse problema de comparações múltiplas em metanálises repetidas ao longo da história. Métodos similares àqueles usados para lidar com o problema de comparações múltiplas gerado por análises interinas num único estudo clínico (alpha spending functions) são utilizados. No entanto, há dificuldades adicionais no contexto de metanálises. O método de ajuste utilizado para lidar com análises interinas num único estudo leva em conta que se sabe a priori qual será o tamanho da amostra do estudo. No caso de metanálises, no entanto, esse tamanho não é conhecido já que não há um planejamento centralizado de todos os estudos sobre uma intervenção que serão realizados ao redor do mundo ao longo de toda a história. Há outras dificuldades importantes no contexto de metanálises, como a heterogeneidade dos estudos incluídos. Na verdade, é um tanto questionável se a técnica de Trial Sequential Analysis deveria mesmo ser utilizada. A Cochrane no momento não recomenda a técnica, com bons argumentos.
Para que a técnica de Trial Sequential Analysis possa ser aplicada, é necessário pensar que o processo de estudo de uma dada intervenção ao longo da história um dia terá um fim, como um estudo clínico específico tem um fim. Além do mais, é necessário estimar quando será esse fim. Isso deve ser feito antes da Trial Sequential Analysis e envolve um método similar ao que é usado para o cálculo amostral para um único estudo. Nesse cálculo, estima-se a quantidade de dados necessária para se obter um certo poder para o teste de hipóteses final. Por exemplo, pode-se estimar a quantidade de dados necessária para que a metanálise final tenha um poder de 90% para detectar uma determinada eficácia, o que significa que haverá uma probabilidade de 10% de não encontrarmos um resultado estatisticamente significativo se a intervenção tiver mesmo aquela eficácia. No caso de metanálises esse cálculo de poder requer uma estimativa não só do tamanho da eficácia que gostaríamos de conseguir detectar, mas também da frequência de eventos e da heterogeneidade entre os estudos. Como os estudos não são planejados pelo autor da metanálise, essas estimativas são difíceis de fazer.
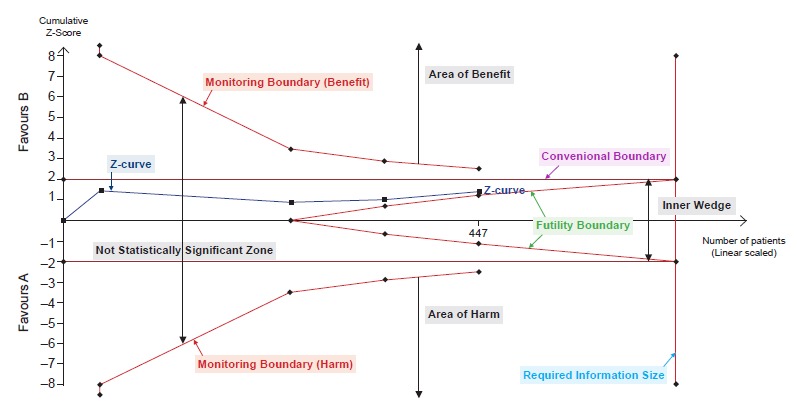
Assim, como no contexto de Trial Sequential Analysis nós imaginamos nossa metanálise como um grande estudo clínico que um dia terá um fim (com um certo tamanho amostral estimado), é comum distinguir resultados positivos ou negativos ainda provisórios de resultados positivos ou negativos definitivos. Um resultado é chamado definitivo quando uma das seguintes situações ocorre: (1) foi atingido o tamanho amostral necessário (segundo as estimativas feitas pelos autores da Trial Sequential Analysis); (2) houve um cruzamento entre a curva que indica os resultados cumulativos dos estudos clínicos conduzidos até agora (a z-curve) e alguma das várias fronteiras de monitoramento (monitoring boundary ou futility boundary — veja figura que ilustra abaixo). Como numa análise interina, um cruzamento desses nos permite declarar ou que a droga funciona (“definitivamente”) ou que devemos parar de estudar a droga por futilidade.